PROYECCIONES ORTOGONALES
En geometría euclidiana, Proyección ortogonal es aquella cuyas rectas proyectantes auxiliares son perpendiculares al plano de proyección (o a la recta de proyección), estableciéndose una relación entre todos los puntos del elemento proyectante con los proyectados.
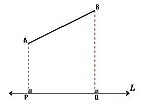
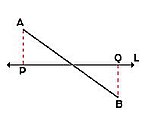
En el plano, la proyección ortogonal es aquella cuyas líneas proyectantes auxiliares son perpendiculares a la recta de proyección L.
Así, dado un segmento AB, bastará proyectar los puntos "extremos" del segmento –mediante líneas proyectantes auxiliares perpendiculares a L–, para determinar la proyección sobre la recta L.
Una aplicación de proyecciones ortogonales son los teoremas de las Relaciones métricas en el triangulo mediante las cuales se puede calcular la dimensión de los lados de un triángulo.
El concepto de proyección ortogonal se generaliza a espacios euclidianos de dimensión arbitraria, inclusive de dimensión infinita. Esta generalización juega un papel importante en muchas ramas de matemática y física.
Casos de proyección ortogonal en el plano
- Proyección ortogonal de un punto
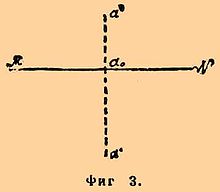
- La proyección ortogonal de un punto P en una recta L es otro punto A que se obtiene trazando una línea auxiliar perpendicular a L desde el punto A. Lógicamente, si el punto P pertenece a la recta L, coinciden: P = A .
- Proyección ortogonal de un segmento
- Caso general: si el segmento dado AB no es paralelo la recta L, la proyección ortogonal es segmento PQ que se obtiene trazando líneas perpendiculares a L desde los puntos extremos. La magnitud de la proyección siempre es menor que la del segmento dado.
- Si el segmento PQ y la recta L son paralelos, la proyección será: AB = PQ, que se obtiene de forma análoga.
- Si el segmento AB tiene un punto común con la recta L, la proyección se obtiene de modo similar.
- Si el segmento AB corta a la recta L, la proyección se obtiene de forma análoga.
- Proyección gráfica
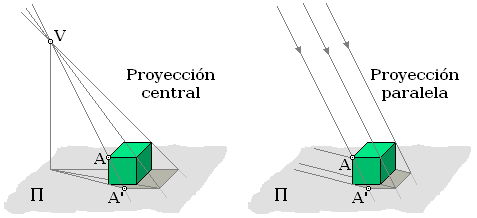
- La proyección gráfica es una técnica de dibujo empleada para representar un objeto en una superficie. La figura se obtiene utilizando líneas auxiliares proyectantes que, partiendo de un punto denominado foco, reflejan dicho objeto en un plano, a modo de sombra.Los elementos principales de la proyección son –como muestran las figuras– el punto de vista o foco de proyección (V), el punto que se desea proyectar (A), el punto proyectado (A'), la línea proyectante (VAA') y el plano sobre el que se proyecta, que recibe diferentes denominaciones como plano de proyección, plano de cuadro o plano imagen (
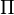 ).
).Proyección Tipo Subtipo Central o perspectiva Varios tipos de perspectiva con puntos de fuga Paralela Ortogonal Isometrica (tres angulos iguales (120º), coef. de reducción iguales) Di métrica (dos ángulos iguales, dos coeficientes distintos) Trimétrica (tres ángulos y coeficientes distintos) Oblicua Perspectiva caballera Proyección centralCuando todas las líneas proyectantes pasan por un punto, se habla de proyección central, cónica o perspectiva, éste es el caso, por ejemplo, de la sombra de un objeto sobre una superficie cuando es alumbrado por una lámpara (foco puntual).Es la adoptada en el sistema de representación cónico, o simplemente perspectiva cónica.Una variante de este sistema de representación lo constituye la proyección estereográfica empleada para la representación plana de la superficie de una esfera, y que se obtiene proyectando todos los puntos de la esfera desde uno de ellos sobre el plano tangente en el punto diametralmente opuesto, o sobre un plano paralelo a este, trazado por el centro de la esfera.Proyección paralelaCuando las líneas proyectantes son paralelas –como el anterior objeto alumbrado por la luz del Sol–, se habla de proyección paralela o proyección cilíndrica. Es un caso particular de proyección central, donde el foco del haz proyectante estaría a distancia infinita.[editar]El sistema diédrico
Es el caso del sistema diédrico, en el que además se cumple que las líneas proyectantes son perpendiculares (ortogonales) al plano de proyección. En este sistema, a diferencia de los demás, no se obtiene una representación volumétrica del objeto en perspectiva, sino su alzado, planta y perfil. A partir de dichas vistas, se puede conseguir una representación tridimensional del objeto en el sistema axonométrico, cuyas líneas proyectantes pueden ser tanto ortogonales como oblicuas, siendo la perspectiva caballera.[editar]El dibujo acotado
Una variante del sistema diédrico,es que, en la práctica, no pueden describirse adecuadamente con los sistemas anteriormente señalados. Son muy utilizados en arquitectura, ingeniería, topografía, entre otrosProyección cónica
Proyección cónica o proyección perspectiva se denomina al sistema de representación gráfico en donde el haz de rayos proyectantes confluye en un punto (el ojo del observador), proyectándose la imagen en un plano auxiliar situado entre el objeto a representar y el punto de vista.Es el sistema de representación que ayuda a reproducir (normalmente en un plano) las imágenes del modo más fiel, con un resultado muy similar a como lo percibimos realmente.Es el sistema empleado en la perspectiva cónica.La proyección cónica se utiliza para elaborar dibujos realistas de objetos, mapas de la Tierra, entre otros.Proyección paralelaEn la geometría Euclidiana, la Proyección paralela es un sistema de representación gráfico para trasponer un objeto tridimensional a un dibujo bidimensional en un plano, llamado plano de proyección. Consiste en proyectar puntos del espacio contra el plano de proyección mediante haces de rectas siempre paralelas entre sí.Esta técnica de representación gráfica se utiliza en diseños de ingeniería y arquitectura ya que su principal ventaja es que mantiene las proporciones relativas de lo representado y se puede medir sobre él directamente. De esta manera se puede reconstruir el objeto fácilmente a partir de representaciones concretas. Proyección oblicuaEn geometría euclidiana, proyección oblicua es aquella cuyas rectas proyectantes auxiliares son oblicuas al plano de proyección, estableciéndose una relación entre todos los puntos del elemento proyectante con los proyectados.En el plano, la proyección oblicua es aquella cuyas líneas proyectantes auxiliares son oblicuas a la recta de proyección.Así, dado un segmento, bastará proyectar los puntos "extremos" del segmento –mediante líneas proyectantes auxiliares oblicuas, para determinar la proyección sobre la recta.
Proyección oblicuaEn geometría euclidiana, proyección oblicua es aquella cuyas rectas proyectantes auxiliares son oblicuas al plano de proyección, estableciéndose una relación entre todos los puntos del elemento proyectante con los proyectados.En el plano, la proyección oblicua es aquella cuyas líneas proyectantes auxiliares son oblicuas a la recta de proyección.Así, dado un segmento, bastará proyectar los puntos "extremos" del segmento –mediante líneas proyectantes auxiliares oblicuas, para determinar la proyección sobre la recta. Geometría de la perspectivaAuxiliados por la geometria, podemos simular el efecto visual de la perspectiva proyectando los objetos tridimensionales sobre un plano (bidimensional) utilizando los métodos de la perspectiva cónica. Recibe este nombre por el hecho de que las líneas paralelas de proyección parten de un punto (a modo de un cono). Mediante este procedimiento se pueden obtener imágenes realistas. Sin embargo, la perspectiva cónica no puede imitar fielmente la visión estereoscópica del ser humano.
Geometría de la perspectivaAuxiliados por la geometria, podemos simular el efecto visual de la perspectiva proyectando los objetos tridimensionales sobre un plano (bidimensional) utilizando los métodos de la perspectiva cónica. Recibe este nombre por el hecho de que las líneas paralelas de proyección parten de un punto (a modo de un cono). Mediante este procedimiento se pueden obtener imágenes realistas. Sin embargo, la perspectiva cónica no puede imitar fielmente la visión estereoscópica del ser humano.[editar]Perspectiva cónica a mano alzada
Estas ayudas para realizar dibujos a mano alzada son de utilidad; pueden ser sencillas y mecánicas, pero también las hay más complejas.Medición a ojo con el lápizUn método sencillo para calcular y comparar proporciones, sobre todo distancias verticales y horizontales, consiste en usar un lápiz como regla. Seleccionamos el objeto que queremos usar como parámetro para nuestro dibujo y luego tomamos un lápiz con la punta para arriba, sin olvidarnos de sostener el brazo bien estirado. Alineamos la punta del lápiz con la parte superior del objeto y el dedo con la parte inferior. Esta medición nos permitirá calcular proporcionalmente los otros objetos. Hemos de estar seguros de que el lápiz se encuentre en posición totalmente vertical a la hora de medir profundidades. Para calcular el grado de inclinación o para medir horizontalmente, el lápiz habrá de estar perpendicular a la línea de visión.Cálculo de un ángulo- Empezaremos con el lápiz en posición horizontal, y luego lo giraremos hasta que se encuentre sobre la línea. Así se determinará el ángulo. Trabajar midiendo a ojo es una técnica muy útil. El diagrama muestra cómo funciona este sistema para emprender un bodegón de un cubo sobre una mesita.
- Si somos diestros, tendremos que mirar por el lado izquierdo del tablero de dibujo, de modo que la mano que dibuja no interfiera con las líneas de mira, perturbando la visión. Con el tablero en posición vertical y con un ojo cerrado, moveremos la cabeza ligeramente hacia la izquierda y hacia la derecha, hasta lograr que el borde del tablero pueda utilizarse como plomada para determinar el tamaño de cada parte de los objetos y, luego, marcaremos estos puntos en el borde del tablero. Esto es particularmente útil para dibujar figuras, pero también puede utilizarse con buenos resultados para dibujar paisajes o, como en este caso, una naturaleza muerta. Es un método consagrado, como lo demuestran las marcas en el borde de muchos dibujos de grandes maestros, lo cual demuestra que dibujaban midiendo a ojo.
- Percibimos los objetos en un plano perpendicular a nuestra línea de visión. Al mirar de frente, el plano será vertical, como si hubiera un cristal suspendido frente a nosotros. Sin embargo, cuando dibujamos, el tablero puede estar inclinado, sobre las rodillas o sobre un caballete, de manera que hemos de mirar hacia abajo y, no obstante, tendemos a visualizar un plano vertical delante de nuestros ojos. Para traducir esta imagen vertical a un tablero colocado en cierto ángulo, debemos ajustar mentalmente las proporciones, cosa ésta que, sin duda, resulta compleja. Corremos el riesgo de ajustar en exceso, haciendo demasiado grande la parte inferior de lo que estamos dibujando. Probablemente para un principiante resulte más sencillo utilizar el tablero vertical, mientras va adquiriendo más práctica y experiencia.
- Existe una excepción natural al uso del tablero vertical, que es cuando se dibuja un tema horizontal (por ejemplo, una naturaleza muerta o un paisaje). En esos casos, es mucho más fácil mirar por encima de la parte superior.
[editar]fvbhi
Perspectivas simplificadas
Otro sistema de representación gráfica es el de proyección paralela (similar a la proyección ortográfica). En este caso, las rectas proyectantes no convergen en un punto, sino que son paralelas, por lo que este sistema suele recibir también el nombre de proyección paralela. Este sistema no refleja fielmente la profundidad del espacio ni la distorsión de los ángulos, sin embargo, conociendo la escala de los ejes ortogonales, permite obtener la verdadera magnitud de los objetos dibujados.[editar]Perspectiva axonométrica
Se pueden dibujar los ejes XYZ desde varias perspectivas, ya que produce un efecto visual particular en cada caso:- Perspectiva isometrica: es una forma de proyección gráfica o, más específicamente, una axonométrica cilíndrica ortogonal. Constituye una representación de un objeto tridimensional en dos dimensiones, en la que los tres ejes de referencia tienen ángulos de 120º, y las dimensiones guardan la misma escala sobre cada uno de ellos. La isometría es una de las formas de proyección utilizadas en dibujo técnico que tiene la ventaja de permitir la representación a escala, y la desventaja de no reflejar la disminución aparente de tamaño -proporcional a la distancia- que percibe el ojo humano.
- Perspectiva caballera: es un sistema de proyección paralela oblicua en el que, por convenio, el plano proyectante es horizontal y las secciones horizontales de los cuerpos representados se proyectan en verdadera magnitud.
- Perspectiva militar, es un caso particular de la perspectiva caballera.
- DIN 5: La perspectiva DIN-5 se corresponde a la UNE 1-031-75 B.
- La perspectiva DIN-5 es la norma que recomienda una perspectiva axonométrica ortogonal dimétrica especifica, que se caracteriza por formar 131º 25' entre los ejes XY y ZY, y 97º 10' entre XZ. Los coeficientes de reducción sobre los ejes X y Z son 2·(raíz cuadrada de 2)/3 = 0'943, y en el eje Y es (raíz cuadrada de 2)/3 = 0'471, siendo la relación entre ellos cx = cz = 2·cy; o bien, ux : uy : uz = 1 : 1/2 : 1.
- Debido a que los ángulos son tan fáciles de medir con un transportador, se suelen dibujar trazando primero el eje Z en vertical y, sobre él, una medida aleatoria (la unidad), a partir de lo cual se traza un triángulo de lados la unidad y una vez y media la unidad.
- El lado del triángulo formado con la unidad es el eje Y, mientras que el eje X es perpendicular al lado formado por una vez y media la unidad. A partir de su extremo.
- Cómo dibujar los ejes XYZ para DIN 5, paso a paso
-
- 1. Medimos una distancia D sobre el eje Z, y denominamos a los extremos A y B.
- 2. Con un compás, trazamos un arco de radio D desde A.
- 3. Con un compás, trazamos un arco de radio D*1.5 desde B.
- 4. En la intersección de los dos arcos, marcamos el punto C.
- 5. El eje Y se obtiene de unir el punto A con el punto C.
- 6. Trazamos un arco de radio D desde C.
- 7. Trazamos un arco de radio D desde B.
- 8. Unimos la intersección de estos dos arcos con A y obtenemos el eje X.
Proyección isométrica
Una proyección isométrica es un método gráfico de representación, más específicamente una axonométrica1 cilíndrica2 ortogonal.3Constituye una representación visual de un objeto tridimensional en dos dimensiones, en la que los tres ejes ortogonales principales, al proyectarse, forman ángulos de 120º, y las dimensiones paralelas a dichos ejes se miden en una misma escala.El término isométrico proviene del idioma griego: "igual medida", ya que la escala de medición es la misma en los tres ejes principales (x, y, z).La isometría es una de las formas de proyección utilizadas en dibujo técnico que tiene la ventaja de permitir la representación a escala, y la desventaja de no reflejar la disminución aparente de tamaño -proporcional a la distancia- que percibe el ojo humano.Visualización
La isometría determina una dirección de visualización en la que la proyección de los ejes coordenados x, y, z conforman el mismo ángulo, es decir, 120º entre sí. Los objetos se muestran con una rotación del punto de vista de 45º en las tres direcciones principales (x, y, z).Esta perspectiva puede visualizarse considerando el punto de vista situado en el vértice superior de una habitación cúbica, mirando hacia el vértice opuesto. los ejes x e y son las rectas de encuentro de las paredes con el suelo, y el eje z, el vertical, el encuentro de las paredes. En el dibujo, los ejes (y sus líneas paralelas), mantienen 120º entre ellos.En perspectiva isométrica se suele utilizar un coeficiente de reducción de las dimensiones equivalente a 0,83. El dibujo isométrico puede realizarse sin reducción, a escala 1:1 o escala natural, y los segmentos del dibujo paralelos a los ejes, se corresponderán con las del objeto.Dentro del conjunto de proyecciones axonométricas o cilíndricas, existen otros tipos de perspectiva, que difieren por la posición de los ejes principales, y el uso de diferentes coeficientes de reducción para compensar las distorsiones visuales.[editar]Aplicaciones
[editar]En el diseño y el dibujo técnico
En diseño industrial se representa una pieza desde diferentes puntos de vista, perpendicular a los ejes coordenados naturales. Una pieza con movimiento mecánico presenta en general formas con ejes de simetría o caras planas. Tales ejes, o las aristas de las caras, permiten definir una proyección ortogonal.Se puede fácilmente dibujar una perspectiva isométrica de la pieza a partir de tales vistas, lo que permite mejorar la comprensión de la forma del objeto.[editar]En arquitectura
Eugène Viollet-le-Duc utilizó este sistema en muchos dibujos de sus edificios, evitando acentuar la importancia de unos volúmenes sobre otros e independizándose del punto de vista del observador.La perspectiva de este dibujo del castillo no es isométrica, si así lo fuera, las torres del castillo estarían dibujadas con la misma altura y diámetro, además las líneas de cumbreras de los tejados serían paralelas entre si, formando un rombo o romboide dependiendo de la planta del castillo.Perspectiva di métrica
La perspectiva dímétrica es una herramienta del dibujo técnico, utilizada para representar volúmenes, que forma parte a su vez de la Axonometría.[editar]Ejes del dibujo y escalas
Los tres ejes principales (ortogonales) que se utilizan para el trazado del dibujo poseen dos ángulos con la misma amplitud y el tercero de amplitud diferente. Los ángulos más usuales para esta perspectiva son 105° y 150°.La construcción de la escala gráfica es similar al de la proyección isométrica, pero que hay que trazar las escalas de los coeficientes de reducción de los dos ejes horizontales.Esta perspectiva o proyección es usual para representar piezas más largas que anchas y altas.
 Perspectiva caballeraLa perspectiva caballera es un sistema de representación que utiliza la proyección paralela oblicua, en el que las dimensiones del plano proyectante frontal, como las de los elementos paralelos a él, están en verdadera magnitud.En perspectiva caballera, dos dimensiones del volumen a representar se proyectan en verdadera magnitud (el alto y el ancho) y la tercera (la profundidad) con un coeficiente de reducción. Las dos dimensiones sin distorsión angular con sus longitudes a escala son la anchura y altura (x, z) mientras que la dimensión que refleja la profundidad (y) se reduce en una proporción determinada. 1:2, 2:3 o 3:4 suelen ser los coeficientes de reducción más habituales.Los ejes X e Z forman un ángulo de 90º, y el eje Y suele tener 45º (o 135º) respecto ambos.Se adoptan, por convención, ángulos iguales o múltiplos de 30º y 45º, dejando de lado 90º, 180º, 270º y 360º por razones obvias.Se puede dibujar fácilmente un volumen a partir de una vista lateral o alzado, trazando a partir de cada vértice líneas paralelas a Y, para reflejar la profundidad del volumen.Este tipo de proyección es frecuentemente utilizada por su facilidad de ejecución, aunque el resultado final no da una imagen tan real como la que se obtendría con una proyección cónica.En Latinoamérica se llama perspectiva caballera a la que utiliza un ángulo de 45º del eje Y respecto del eje X y ninguna reducción.Trazado de la perspectiva caballeraPara el trazado de la perspectiva caballera, empleando una escuadra, se coloca una regla inclinada a 45º que sirve de referencia para apoyar la escuadra sobre el lado adecuado según la inclinación de la recta a trazar. Las líneas de fuga de la perspectiva caballera, se trazan perpendiculares a la regla.Si sobre los ejes ponemos las coordenadas de un punto, haciendo las paralelas correspondientes a los ejes, situamos en punto en el espacio, según la perspectiva caballera.
Perspectiva caballeraLa perspectiva caballera es un sistema de representación que utiliza la proyección paralela oblicua, en el que las dimensiones del plano proyectante frontal, como las de los elementos paralelos a él, están en verdadera magnitud.En perspectiva caballera, dos dimensiones del volumen a representar se proyectan en verdadera magnitud (el alto y el ancho) y la tercera (la profundidad) con un coeficiente de reducción. Las dos dimensiones sin distorsión angular con sus longitudes a escala son la anchura y altura (x, z) mientras que la dimensión que refleja la profundidad (y) se reduce en una proporción determinada. 1:2, 2:3 o 3:4 suelen ser los coeficientes de reducción más habituales.Los ejes X e Z forman un ángulo de 90º, y el eje Y suele tener 45º (o 135º) respecto ambos.Se adoptan, por convención, ángulos iguales o múltiplos de 30º y 45º, dejando de lado 90º, 180º, 270º y 360º por razones obvias.Se puede dibujar fácilmente un volumen a partir de una vista lateral o alzado, trazando a partir de cada vértice líneas paralelas a Y, para reflejar la profundidad del volumen.Este tipo de proyección es frecuentemente utilizada por su facilidad de ejecución, aunque el resultado final no da una imagen tan real como la que se obtendría con una proyección cónica.En Latinoamérica se llama perspectiva caballera a la que utiliza un ángulo de 45º del eje Y respecto del eje X y ninguna reducción.Trazado de la perspectiva caballeraPara el trazado de la perspectiva caballera, empleando una escuadra, se coloca una regla inclinada a 45º que sirve de referencia para apoyar la escuadra sobre el lado adecuado según la inclinación de la recta a trazar. Las líneas de fuga de la perspectiva caballera, se trazan perpendiculares a la regla.Si sobre los ejes ponemos las coordenadas de un punto, haciendo las paralelas correspondientes a los ejes, situamos en punto en el espacio, según la perspectiva caballera.Perspectiva militar
La perspectiva militar o cabinet es una proyección paralela oblicua, un sistema de representación por medio de tres ejes cartesianos (X, Y, Z).En el dibujo, el eje Z es el vertical, mientras que los otros dos (X, Y) forman 90° entre sí, determinando el plano horizontal (suelo). Normalmente, el eje X se encuentra a 120° del eje Z, mientras que eje Y se encuentra a 150° de dicho eje.La principal ventaja radica en que las distancias en el plano horizontal conservan sus dimensiones y proporciones. Las circunferencias en el plano horizontal se puede trazar con compás, pues no presentan deformación. Las circunferencias en los planos verticales se representan como elipses.Para la realización del dibujo, se aplica un coeficiente de reducción en los ejes cartesianos. En la perspectiva militar el eje afectado es el eje Z, presentando una reducción de 2/3. Los otros dos ejes (X, Y) no tienen reducción.La perspectiva militar es un sistema de representación hipotético, debido a que la única forma de que presenten 90° los ejes X e Y, sólo sería mirando el cuerpo desde arriba. Trazado de la perspectiva militarEl uso del cartabón el eje z es vertical, el eje x forma un ángulo de 30º con la horizontal, y el eje y es perpendicular al eje x, esto es forma un ángulo de 60º con la horizontal, por tanto coinciden con las características del cartabón, como podemos ver.Poniendo una regla horizontal podemos trazar el eje vertical empleando el ángulo recto del cartabón, con el vértice de 30º trazamos el eje x, y perpendicular a el con el vértice de 60º el eje y.Situando las coordenadas de un punto sobre los ejes, y trazando las rectas paralelas oportunas podemos ver la perspectiva del punto según el sistema militar.Perspectiva trimétrica
Trazado de la perspectiva militarEl uso del cartabón el eje z es vertical, el eje x forma un ángulo de 30º con la horizontal, y el eje y es perpendicular al eje x, esto es forma un ángulo de 60º con la horizontal, por tanto coinciden con las características del cartabón, como podemos ver.Poniendo una regla horizontal podemos trazar el eje vertical empleando el ángulo recto del cartabón, con el vértice de 30º trazamos el eje x, y perpendicular a el con el vértice de 60º el eje y.Situando las coordenadas de un punto sobre los ejes, y trazando las rectas paralelas oportunas podemos ver la perspectiva del punto según el sistema militar.Perspectiva trimétrica
La perspectiva trimétrica es una proyeccion axonométrica, para representar volúmenes, en la cual el objeto tridimensional se encuentra inclinado con respecto al «plano del cuadro» de forma que sus tres ejes principales experimentan reducciones diferentes. Proyección cartográficaLa proyección cartográfica o proyección geográfica es un sistema de representación gráfico que establece una relación ordenada entre los puntos de la superficie curva de la Tierra y los de una superficie plana (mapa). Estos puntos se localizan auxiliándose en una red de meridianos y paralelos, en forma de malla. La única forma de evitar las distorsiones de esta proyección sería usando un mapa esférico pero, en la mayoría de los casos, sería demasiado grande para que resultase útil.En un sistema de coordenadas proyectadas, los puntos se identifican por las coordenadas x,y en una malla cuyo origen depende de los casos. Este tipo de coordenadas se obtienen matemáticamente a partir de las coordenadas geográficas (longitud y latitud), que son no proyectadas.Las representaciones planas de la esfera terrestre se llaman mapas, y los encargados de elaborarlos o especialistas en cartografía se denominan cartógrafos.
Proyección cartográficaLa proyección cartográfica o proyección geográfica es un sistema de representación gráfico que establece una relación ordenada entre los puntos de la superficie curva de la Tierra y los de una superficie plana (mapa). Estos puntos se localizan auxiliándose en una red de meridianos y paralelos, en forma de malla. La única forma de evitar las distorsiones de esta proyección sería usando un mapa esférico pero, en la mayoría de los casos, sería demasiado grande para que resultase útil.En un sistema de coordenadas proyectadas, los puntos se identifican por las coordenadas x,y en una malla cuyo origen depende de los casos. Este tipo de coordenadas se obtienen matemáticamente a partir de las coordenadas geográficas (longitud y latitud), que son no proyectadas.Las representaciones planas de la esfera terrestre se llaman mapas, y los encargados de elaborarlos o especialistas en cartografía se denominan cartógrafos. Propiedades de la proyección cartográficaSe suelen establecer clasificaciones en función de su principal propiedad; el tipo de superficie sobre la que se realiza la proyección: cenital (un plano), cilíndrica (un cilindro) o cónica (un cono); así como la disposición relativa entre la superficie terrestre y la superficie de proyección (plano, cilindro o cono) pudiendo ser tangente, secante u oblicua. Según la propiedad que posea una proyección puede distinguirse entre:
Propiedades de la proyección cartográficaSe suelen establecer clasificaciones en función de su principal propiedad; el tipo de superficie sobre la que se realiza la proyección: cenital (un plano), cilíndrica (un cilindro) o cónica (un cono); así como la disposición relativa entre la superficie terrestre y la superficie de proyección (plano, cilindro o cono) pudiendo ser tangente, secante u oblicua. Según la propiedad que posea una proyección puede distinguirse entre:- proyecciones equidistantes, si conserva las distancias.
- proyecciones equivalentes, si conservan las superficies.
- proyecciones conformes, si conservan las formas (o, lo que es lo mismo, los ángulos).
No es posible tener las tres propiedades anteriores a la vez, por lo que es necesario optar por soluciones de compromiso que dependerán de la utilidad a la que sea destinado el mapa.Tipos de proyecciones cartográficasDependiendo de cuál sea el punto que se considere como centro del mapa, se distingue entre proyecciones polares, cuyo centro es uno de los polos; ecuatoriales, cuyo centro es la intersección entre la línea del Ecuador y un meridiano; y oblicuas o inclinadas, cuyo centro es cualquier otro punto.Se distinguen tres tipos de proyecciones básicas: cilíndricas, cónicas y azimutales.[editar]Proyección cilíndrica
La proyección de Mercator es un tipo de proyección cartográfica cilíndrica, ideada por Gerardus Mercator en 1569, para elaborar planos terrestres. Es muy utilizada en planos de navegación por la facilidad de trazar rutas de rumbo constante o loxodrómicas.Mercator, mediante proyección, pretende representar la superficie esférica terrestre sobre una superficie cilíndrica, tangente al ecuador, que al desplegarse genera un mapa terrestre plano.Es un modelo idealizado que trata a la tierra como un globo hinchable que se introduce en un cilindro y que empieza a «inflarse» ocupando el volumen del cilindro, imprimiendo el mapa en su cara exterior. Este cilindro cortado longitudinalmente y desplegado sería parecido al mapa con la proyección de Mercator.Esta proyección presenta una buena aproximación en su zona central, pero las zonas superior e inferior correspondientes a norte y sur presentan grandes deformaciones. Los mapas con esta proyección se utilizaron en la época colonial con gran éxito. Europa era la potencia dominante de la época, y para los que viajaban hacia el nuevo mundo por las zonas ecuatoriales, no tenía gran importancia la deformación que poseíanProyección de Peters
La Proyección de Peters (llamada así por Arno Peters), aunque más correctamente Proyección de Gall-Peters, es una proyección cartográfica que apareció por primera vez en 1856, publicada en el Polish Geographical Magazine por [James Gall].Esta proyección la popularizó Arno Peters, que era cartógrafo, en una rueda de prensa que dio en 1976, tratando de denunciar las implicaciones políticas de la proyección de Mercator. Sin embargo, se trataba de una proyección casi idéntica a la elaborada en 1856 por James Gall, un religioso escocés. La Unesco y muchas ONG la adoptaron y popularizaron desde entonces, convirtiéndose en la visión políticamente correcta del mapamundi, aunque es muy controvertida pues los cartógrafos por lo general no la han tomado en consideración (Peters no era cartógrafo).En ella los paralelos y los meridianos son sustituidos por una cuadrícula de 10 grados decimales. La proyección refleja correctamente las áreas de los países (es «equiareal»), pero no sus siluetas, la mayoría de las cuales aparecían demasiado estiradas. Los meridianos aparecen como líneas verticales paralelas y los paralelos como líneas horizontales paralelas que van acortando la distancia entre ellas hacia los polos. Las formas de las áreas tropicales y subtropicales aparecen más estrechas y alargadas y las áreas de altas latitudes aparecen más ensanchadas y más achatadas que en otras proyecciones más habituales[editar]Proyección cónica
La proyección cónica se obtiene proyectando los elementos de la superficie esférica terrestre sobre una superficie cónica tangente, situando el vértice en el eje que une los dos polos. Aunque las formas presentadas son de los polos, los cartógrafos utilizan este tipo de proyeccion para ver los países y continentes.Proyección cónica simple
La proyección cónica simple se obtiene proyectando los elementos de la superficie esférica terrestre sobre una superficie cónica secante, tomando el vértice en el eje que une los dos polos.La proyección cónica simple puede tener uno o dos paralelos de referencia.Proyección conforme de Lambert
La proyección conforme cónica de Lambert es una proyección cartográfica cónica que es frecuentemente usada en navegación aérea.No debe ser confundida con la proyección azimutal de Lambert.En esencia, la proyección superpone un cono sobre la esfera de la Tierra, con dos paralelos de referencia secantes al globo e intersecándolo. Esto minimiza la distorsión proveniente proyectar una superficie tridimensional a una bidimensional. La distorsión es mínima a lo largo de los paralelos de referencia, y se incrementa fuera de los paralelos elegidos. Como el nombre lo indica, esta proyección es conforme.Los pilotos utilizan estas cartas debido a que una línea recta dibujada sobre una carta cuya proyección es conforme cónica de Lambert muestra la distancia verdadera entre puntos. Sin embargo, los aviones deben volar rutas que son arcos de círculos máximos para recorrer la distancia más corta entre dos puntos de la superficie, que en una carta de Lambert aparecerá como una línea curva que debe ser calculada en forma separada para asegurar de identificar los puntos intermedios correctos en la navegación.Sobre la base de la proyección Proyección cónica simple con dos meridianos de referencia Lambert ajustó matemáticamente la distancia ente paralelos para crear un mapa conforme. Como los meridianos son líneas rectas y los paralelos arcos de círculo concéntricos las diferentes hojas encajan perfectamente Esta proyección consiste en utilizar no un cono, sino varios superpuestos. El resultado es un mapa dividido en franjas. El único meridiano que tendrá la mismaescala es el central, que aparece como una línea recta. Los demás meridianos son curvas, y la escala aumenta con la distancia. También el ecuador es una línea recta, perpendicular al meridiano central. Los demás paralelos son arcos concéntricos.Esta proyección ni es conforme ni conserva las áreas, pero en la zona central las variaciones de escala son mínimas
Esta proyección consiste en utilizar no un cono, sino varios superpuestos. El resultado es un mapa dividido en franjas. El único meridiano que tendrá la mismaescala es el central, que aparece como una línea recta. Los demás meridianos son curvas, y la escala aumenta con la distancia. También el ecuador es una línea recta, perpendicular al meridiano central. Los demás paralelos son arcos concéntricos.Esta proyección ni es conforme ni conserva las áreas, pero en la zona central las variaciones de escala son mínimas[editar]Proyección azimutal, cenital o polar
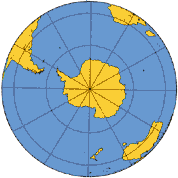
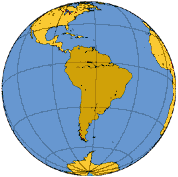
En este caso se proyecta una porción de la Tierra sobre un plano tangente al globo en un punto seleccionado, obteniéndose una imagen similar a la visión de la Tierra desde un punto interior o exterior. Si la proyección es del primer tipo se llama proyección gnomónica; si es del segundo, ortográfica. Estas proyecciones ofrecen una mayor distorsión cuanto mayor sea la distancia al punto tangencial de la esfera y el plano. Este tipo de proyección se relaciona principalmente con los polos y hemisferios.Proyección ortográfica
Proyección estereográficaLa proyección ortográfica es un sistema de representación gráfica, consistente en. representar elementos geométricos o volúmenes en un plano, medianteproyección ortogonal; se obtiene de modo similar a la "sombra" generada por un "foco de luz" procedente de una fuente muy lejana. Su aspecto es el de una fotografía de la Tierra.La proyección polar se caracteriza porque todos los meridianos son líneas rectas y la distancia entre paralelos disminuye según nos alejamos del centro. La distancia entre paralelos o meridianos depende de la escala así que cuando disminuye la distancia disminuye la escala y cuando aumenta la distancia aumenta la escala.
La proyección ecuatorial se caracteriza porque los paralelos son líneas rectas. También es una línea recta el meridiano central. A medida que nos alejamos del centro la escala disminuye. Los meridianos tienen forma de arco.
La proyección oblicua también se caracteriza por que los paralelos y los meridianos se acercan a medida que se alejan del centro.
Proyección gnomónicaLa proyección estereográfica es un sistema de representación gráfico en el cual se proyecta la superficie de una esfera sobre un plano mediante haces de rectas que pasan por un punto, o foco. El plano de proyección es tangente a la esfera, o paralelo a éste, y el foco es el punto de la esfera diametralmente opuesto al punto de tangencia del plano con la esfera.La superficie que puede representar es mayor que un hemisferio. El rasgo más característico es que la escala aumenta a medida que nos alejamos del centro.En su proyección polar los meridianos son líneas rectas, y los paralelos son círculos concéntricos. En la proyección ecuatorial sólo son líneas rectas el ecuadory el meridiano central.Existe otro tipo de proyección estereográfica que es útil para representar la esfera celeste. En este caso, como los puntos a proyectar están fuera de la esfera, el primer paso es proyectarlos a la esfera uniéndolos con su centro. Una vez los puntos externos están proyectados en la superficie de la esfera, el procedimiento es análogo al explicado anteriormente. Usualmente, el plano es uno horizontal que contiene al centro de la esfera, y el foco de la proyección es el nadir.Lo característico de esta proyección es que es más subjetiva, porque propone la posición del observador P en el centro y representa directamente mediante coordenadas locales el acimut y altura del punto A en la esfera celeste. Se utiliza en arquitectura e ingeniería para representar la posición del Sol a lo largo del año, y calcular asoleamientos y sombras que produce.
La proyección gnomónica (denominada también como proyección central1 ) es unaproyección geográfica caracterizada por tener simetría radial alrededor del punto central (perspectiva centrográfica). Es decir, mediante esta proyección, cualquier punto de una esfera es conectada desde su centro por por una línea hasta que interseca en un plano tangente a la esfera (denominado plano de proyección).Concepto
Se puede imaginar como la proyección de un foco de luz sobre un plano tangencial a la Tierra, en el que el foco de luz se sitúa en el centro de la Tierra. La escala aumentará rápidamente del centro al exterior. Con este concepto los círculos máximos se proyectan como líneas rectas en el plano de proyección. El círculo máximo y el punto central forman un plano que interseca en una línea recta en el plano de proyección. Los círculos menores forman secciones cónicas en el plano de proyección. Esto es debido a que los círculos menores forman con el centro de la esfera uncono mediante las generatrices, la intersección del cono forma las cónicas correspondientes.[editar]Usos
La proyección gnomónica posee varias utilidades en el terreno de la cartografía (mediante el trazado de las cartas gnomónicas) y en gnomónica en el trazado y diseño de algunos relojes solares.[editar]Cartografía
Véase también: CartografíaEn las cartas gnomónicas elaboradas mediante esta proyección toda línea recta es un círculo máximo terrestre y el camino más corto entre dos puntos de la Tierra. Es decir forma un meridiano o los paralelos. Se usa en la navegación aeronáutica para trazar los rumbos verdaderos. Con este sistema no se puede representar un hemisferio completo.En la proyección polar todos los meridianos son líneas rectas y se disponen radialmente, en la proyección ecuatorial son líneas rectas elecuador y los meridianos, que se disponen verticalmente, en la proyección oblicua son líneas rectas el ecuador y los meridianos.Proyección azimutal de LambertLa Proyección acimutal equivalente de Lambert conserva deliberadamente las áreas.No debe ser confundida con la Proyección Conforme Cónica de Lambert que es muy utilizada en navegación aérea. La proyección azimutal equivalente de Lambert no es conforme, es decir, no mantiene el valor real de los ángulos tras realizar la proyección. La escala disminuye a medida que nos acercamos al borde exterior, pero en menor medida que en la Proyección ortográfica. Este sistema es muy adecuado para trazar mapas de pequeña escala.Historia
El inventor de esta proyección es el matemático alemán Johann Heinrich Lambertque en el año 1759 publicó un libro con reflexiones diversas acerca de la proyección, el escrito se titulaba "Freye Perspective" (hubo en 1774 una segunda edición mejorada). Los escritos de perspectiva y proyección fueron ampliados en 1943 por Max Steck reuniéndolos en una obra completa.[editar]Formulación
La distancia desde el punto de tangencia sobre el mapa es proporcional a la distancia en línea recta sobre la superficie de la tierra: r(d) = c sin (d/2R).[editar]Ventajas de la proyección
Este sistema de proyección presenta como gran ventaja que las áreas representadas en los mapas no sufren deformación y son proporcionales a las formas originales, cumpliéndose la regla siguiente: "superficies iguales representan ángulos sólidos iguales".[editar]Proyecciones modificadas
En la actualidad la mayoría de los mapas se hacen a base de proyecciones modificadas o combinación de las anteriores, a veces, con varios puntos focales, a fin de corregir en lo posible las distorsiones en ciertas áreas seleccionadas, aún cuando se produzcan otras nuevas en lugares a los que se concede importancia secundaria, como son por lo general las grandes extensiones de mar. Entre las más usuales figuran la proyección policónica de Lambert utilizada para fines educativos, y los mapamundis elaborados según las proyecciones Winkel-Tripel (adoptada por la National Geographic Society1 ) y Mollweide, que tienen forma de elipse y menores distorsiones.[editar]Proyecciones convencionales
Las proyecciones convencionales generalmente fueron creadas para representar el mundo entero (mapamundi) y dan la idea de mantener las propiedades métricas, buscando un balance entre distorsiones, o simplemente hacer que el mapamundi "se vea bien". La mayor parte de este tipo de proyecciones distorsiona las formas en las regiones polares más que en el ecuador:- Proyección de Aitoff
- Proyección de Bernard J.S. Cahill
- Proyección de Dymaxion
- Proyección de Goode
- Proyección de Kavrayskiy VII
- Proyección cilíndrica de Miller
- Proyección de Robinson
- Proyección de Van der Grinten
- Proyección de Wagner VI
- Proyección de Waterman
- Proyección de Winkel-Tripel
[editar]
Sistema diédricoEl sistema diédrico es un método de representación geométrico de los elementos del espacio tridimensional sobre un plano, es decir, la reducción de las tres dimensiones del espacio a las dos dimensiones del plano, utilizando una proyección ortogonal sobre dos planos que se cortan perpendicularmente. Para generar las vistas diédricas, uno de los planos se abate sobre el segundo. .Es un método gráfico de representación que consiste en obtener la imagen de un objeto (en planta y alzado), mediante la proyección de haces perpendiculares a dos planos principales de proyección, horizontal (PH) y vertical (PV). El objeto queda representado por su vista frontal (proyección en el plano vertical) y su vista superior (proyección en el plano horizontal); también se puede representar su vista lateral, como proyección auxiliar.
Si se prescinde de la línea de tierra, se denomina sistema diédrico directo.IntroducciónLa geometría descriptiva es la ciencia que trata la manera de representar una figura de dos o tres dimensiones en un plano. El sistema básico dentro de esta geometría es el sistema diédrico o de proyecciones diédricas ortogonales. Gaspard Monge, geómetra francés, fue quien codificó su estudio y mecanismo; para ello nos valemos de dos planos proyectantes que forman entre sí un ángulo recto o ángulo perfecto (de 90º).[editar]
Planos proyectantes principalesLos dos planos proyectantes principales son el Horizontal y el Vertical. Su intersección se denomina Línea de tierra.- Plano Horizontal (PH): contiene la proyección horizontal o planta. Está subdividido por la Línea de tierra (LT) en: Plano Horizontal Posterior (detrás) y Plano Horizontal Anterior (delante).
- Plano Vertical (PV): contiene la proyección vertical o alzado. Está subdividido por la Línea de Tierra en: Plano Vertical Superior (arriba) y Plano Vertical Inferior (abajo).
Normalmente, sólo se usan los planos PH y PV, que se cortan en la Línea de tierra (LT) dando origen a una subdivisión del espacio en cuatro ángulos diedros o cuadrantes.También se utiliza, como plano auxiliar, el denominado:- Plano de Perfil (PP): contiene la proyección lateral izquierda (o derecha).
- Planos bisectores
Los dos planos bisectores son aquellos que dividen a los cuadrantes en dos octantes de 45º cada uno. El primer bisector está en el primero y tercer cuadrante y el segundo bisector en el segundo y cuarto cuadrante.Para representar en dos dimensiones (sobre un papel) las vistas principales en el sistema diédrico, se realiza un abatimiento, que consiste en girar, tumbar, o abatir un plano principal de tal manera que el Plano Horizontal (PH) se superponga al Plano Vertical (PV).Un punto situado en el espacio se representa mediante sus dos proyecciones (a modo desombras) sobre los planos principales: proyección horizontal y proyección vertical.- Cota
Se denomina cota de un punto del espacio a la distancia entre él y su proyección en el plano horizontal, o lo que es lo mismo la distancia entre la proyección vertical y la línea de Tierra (LT).- Alejamiento
Se denomina alejamiento de un punto del espacio a la distancia entre él y su proyección en el plano vertical, que equivale a la distancia entre la proyección horizontal y la línea de Tierra (LT).- Determinación por coordenadas
Un punto puede determinarse por coordenadas. El origen de este sistema será la intersección de los planos principales: horizontal, vertical y de perfil.- El eje X está determinado por la recta intersección de los planos horizontal y vertical, es decir, sobre la Línea de tierra.
- El eje Y está determinado por la recta intersección de los planos horizontal y de perfil.
- El eje Z está determinado por la recta intersección de los planos vertical y de perfil.
Una recta está definida cuando se conocen sus dos proyecciones, horizontal y vertical. La proyección de una recta sobre un plano es otra recta, formada por la proyección de todos los puntos de ella. Conociendo las parejas de proyecciones de dos puntos de una recta, se obtiene la proyección uniéndolos.- Trazas de una recta
Las trazas de una recta son los puntos de intersección con los planos principales (PV y PH)[editar]
Representación de un volumen geométricoUn cuerpo geométrico se representa mediante la proyección de sus aristas, sus generatrices extremas, o su contorno (esfera). Las aristas o generatrices más próximas al punto de vista se representan como segmentos de trazo continuo, y las posteriores, u ocultas, mediante segmentos de trazo discontinuo. Las zonas seccionadas se indican mediante trazos paralelos inclinados.[editar]
Representación de una circunferenciaLa proyección de una circunferencia es, generalmente, una elipse. Será otra circunferencia semejante si está contenida en un plano paralelo a uno principal. Puede ser un segmento si está de perfil respecto de un plano principal, siendo su longitud la del diámetro.[editar]
Diferentes sistemasSegún como estén reflejadas las proyecciones en el plano del dibujo, existen dos sistemas de representación:- Sistema europeo: Las proyecciones se recogen tras el objeto. Son vistas en el primer cuadrante.
- Sistema americano: Las proyecciones se reflejan desde el objeto. Son vistas en el tercer cuadrante.
Aunque en ambos sistemas las proyecciones (representaciones del objeto) son exactamente las mismas, su disposición en el plano del dibujo es la inversa.


































excelente información, ahora lo plasmaré para mis estudiantes del 4to. grado
ResponderEliminarBN Informacion gracias me ayudo mucho en mi materia Att:Kleynore23
ResponderEliminaramigo muchas gracias me ayudo mucho con mi tarea de dibujo tecnico. de verdad muchas gracias :-) :) c:
ResponderEliminarmuy bien pero no vuelvas a copiar cosas de wikipedia
ResponderEliminarjajajja tienes razon pero si es buena la informacion
EliminarExcelente
ResponderEliminarEs una copia de wikipedia :v
ResponderEliminarCaleb estuvo aqui
ResponderEliminar:v
ResponderEliminarViva la mejor escula I.P.E.T. N° 267 "Antonio Graziano"
ResponderEliminarruth es bella
ResponderEliminarmucho texto pero gracias pibe B)
ResponderEliminar